Three-dimensional model of the human ear using finite element method to study the effects of bone and cartilage on umbo displacement

Lucrece Barbara Penpen Komgue ^1,2,*, Safaa Assif ², Adil Faiz ¹, Joël Ducourneau ¹, and Abdelowahed Hajjaji ²

1 Laboratory of Energetics and Theoretical and Applied Mechanics, Lorraine University, Nancy, France

2 Laboratory of Engineering Sciences for Energy, National School of Applied Sciences, El Jadida, Morocco

* penpenkomguelucrece@gmail.com

Abstract: The three-dimensional modeling of the human ear has emerged as a relevant alternative to experiments conducted on cadavers, owing to its accessibility while providing comparable benefits for students (Jenks et al., 2021). Two primary methods for generating 3D computer models of the human ear are documented in the literature: the µCT imaging method and the finite element method, which is based on a numerical approach.

The µCT (Micro-computed tomography) imaging approach involves performing high-resolution scans at a microscopic scale of the human ear using X-rays, with the aim of reconstructing it in two or three dimensions. In contrast, the finite element method employs documented dimensions and geometric shapes from existing literature to model the human ear using work plans.

The present study will concentrate on the finite element method. It is imperative to acknowledge that most of the three-dimensional models of the human ear cited in the extant literature do not account for bony and cartilaginous structures (Gan et al., 2004), (Zhang and Gan, 2013), (Liu et al., 2022).

This research aims to develop a comprehensive three-dimensional model of the human external ear, which includes the auditory canal, skin, bone, cartilage, and tympanic membrane. This model is intended to facilitate an examination of how bone and cartilage influence the displacement of the umbo. In this constructed model, both the ossicular chain and cochlea were substituted with a mechanical impedance represented by a mass-spring-damper system.

The findings from this study suggest that both bone and cartilage contribute to the displacement of the umbo within a frequency range of 2500 to 6300 Hz.

Keywords: Three-dimensional modeling, Finite Element Methods, human ear, displacement of the umbo.

Received: April 08, 2025

Revised: May 21, 2025

Accepted: June 06, 2025

Published: July 25, 2025

Citation: Senhaji A. Interoperability of Health Systems: Challenges and Perspectives for Improving Care. Moroccan Journal of Health and Innovation (MJHI) 2025, Vol 1, No 2. https://mjhi-smb.com

Copyright: © 2025 by the authors.

1. Introduction

The human ear serves as the organ responsible for auditory perception. Its primary function encompasses the amplification, transmission, and conversion of acoustic waves from the environment into electrical impulses that are subsequently interpreted by the brain through the auditory nerve. The structure of the ear can be categorized into three distinct sections: the outer ear, which includes the pinna and external auditory canal; the middle ear, consisting of the tympanic membrane and ossicular chain (comprising malleus, incus, and stapes); and the inner ear, which incorporates both the vestibular system and cochlea.

In the literature, two principal approaches are described for three-dimensional geometric modeling of the human ear: one based on imaging scans and another grounded in finite element methods.

The imaging scan approach entails capturing high-resolution scans of the human ear at a microscopic scale using X-rays to reconstruct its geometric shape in two or three dimensions. Conversely, the finite element method relies on solving differential equations and utilizes documented dimensions and geometric descriptions of the human ear found in literature to model its geometric form.

Regardless of the modeling approach employed, the three-dimensional (3D) modeling of the human ear has emerged as a significant alternative to experiments conducted on cadavers, owing to its accessibility while providing comparable benefits for students. In addition to its educational contributions, 3D modeling of the human ear facilitates various studies regarding the functioning of the auditory system, as well as examining the impact of auditory prosthetics on this system.

In the present study, we will concentrate on employing the finite element method for modeling purposes. Existing literature reveals that the majority of three-dimensional models of the human ear created using this methodology do not incorporate bony and cartilaginous tissues (Gan et al., 2004), (Zhang and Gan, 2013), (Liu et al., 2022).

2. Finite element model

Our approach to creating the 3D human ear model involved the following. The auditory canal was modeled using cross-sections with variable diameters and orientations (Figure 1.a). By applying the loft operation to all the cross-sections defining the auditory canal, a 3D geometry of an “S” shaped canal was generated (Figure 1.b). Both parts of the tympanic membrane were modeled. Its geometry is conical (Daphalapurkar et al., 2009), with a surface area of 123.5 mm², a uniform thickness of 0.1 mm, a height of 1.7 mm (Lee et al., 2006), (Wever and Lawrence, 1954) (Figure 2.a), and it forms an inclination angle of 50 degrees with the auditory canal (Stinson and Lawton, 1989) (Figure 2.b). The skin was modeled with a decreasing thickness ranging from 1 mm to 0.8 mm at the cartilaginous part and from 0.8 mm to 0.5 mm at the bony part (Ballachanda, 2013), (Perry and Shelley, 1955), (Brummund et al., 2014) (Figure 3.a). The cartilage was modeled over a length of 15 mm from the entrance of the canal, exhibiting a decreasing thickness from 13.6 mm to 8 mm relative to the auditory canal (Figure 3.b). The bone was modeled over the other half of the auditory canal, showing a varying thickness from 6.9 mm to 8.8 mm relative to the auditory canal (Figure 3.c).

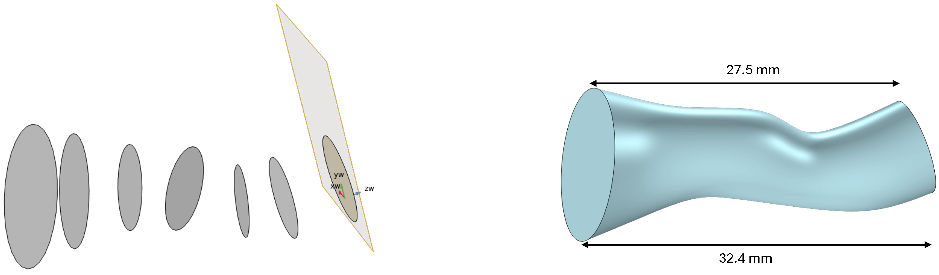
Figure 1. Geometric model and dimensions of the auditory canal.

Figure 2.  Geometric model and dimensionsof the eardrum.

Figure 3. Geometric model and dimensions of (a) the skin, (b) cartilage and (c) bone.

Figure 4. 3D model of the human ear.

3. Boundary conditions

For this study, the auditory canal was defined as a fluid domain filled with air. The skin, bone, cartilage, and tympanic membrane were delineated as solid domains.

To restrict any movement in space, the tympanic ring, the circumferential boundaries of the skin, bone, and cartilage were fixed using a fixed constraint displacement (u_x=u_y=u_z=0).

The loading of the ear components located directly after the tympanic membrane (the malleus, incus, stapes and cochlea) has been replaced by an equivalent mechanical impedance represented by a mass-spring-damper system. For this mechanical impedance, the value of the spring constant ‘K’ and the friction coefficient ‘d’ used are respectively 120 N/m and 0.2 N·s/m.

A plane wave of 0.2 Pa corresponding to 80 dB was applied at the entrance of the auditory canal. The interfaces between the solid domains and the auditory canal were expressed through acoustic-structural coupling.

Material properties

The materials’ properties have been taken from the literature and are presented in Table 1.

Table 1: Material properties of the proposed model

		Young’s modulus (MPa)	Density (kg/m3)	Poisson’s ratio	Loss factor
Bone	Value	11316	1714	0.3	0.01
	Reference	(Shaw and Stinson, 1981)	(Shaw and Stinson, 1981)	(Delille et al., 2007)	n/a
Cartilage	Value	7.2	1080	0.26	0.05
	Reference	(Peterson and  Dechow, 2003)	(Grellmann et al., 2006)	(Peterson and  Dechow, 2003)	n/a
Skin	Value	0.5	1100	0.4	0.1
	Reference	(Cox and Peacock, 1979)	(Sarvazyan et al., 1995)	n/a	n/a
Tympanic membrane	Value	33.3	1200	0.3	–
	Reference	(Cameron, 1991)	(Cameron, 1991)	n/a	–

The auditory canal is defined as an air-filled domain with a density of ρ_air = 1.20 kg/m³ and a speed of sound of c_air = 343.2 m/s.

4. Results and interpretations

In this section, we will examine the impact of bone and cartilage on the displacement of the umbo.

Here, we examine two configurations. The first is that of a 3D model of the human ear, as described in section 2. For reference, this foundational model comprises the auditory canal, cartilage, skin, bone, and tympanic membrane. To investigate the influence of bone and cartilage on umbo displacement within the proposed model, we removed the skin, bone, and cartilage from the proposed model. Subsequently, we substituted the skin with a physiological impedance.

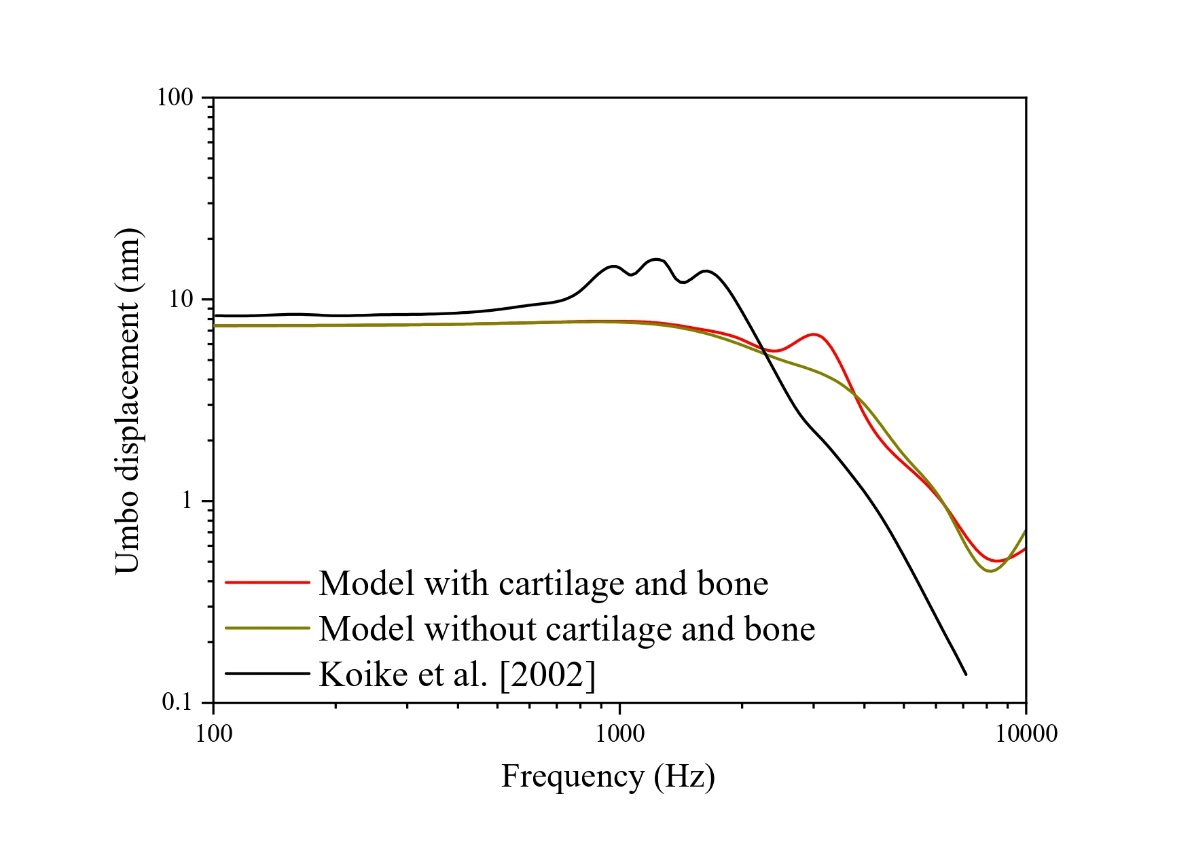
Figure 5. Umbo displacement at 80 dB SPL.

This figure presents the comparative results of the displacement of the umbo induced by an acoustic pressure of 80 dB at the entrance of the ear canal. In this figure, we have the results of the 3D model of the human ear developed with or without bony and cartilaginous tissues, and the results of Koike et al. (Koike et al., 2002).

First, we have a comparison between the results of the 3D model of the human ear developed when the cartilaginous and bony tissues are taken into account or not. The comparison of these two results highlights the effect of bone and cartilage on the displacement of the umbo. Indeed, we find that bony and cartilaginous tissues have a frequency range of interest between 2500 and 6300 Hz.

Secondly, we have a comparison between the results of our model and those of Koike et al. (Koike et al., 2002). This comparative study allows us first to validate the modeling approach, the geometric dimensions, and the parameters used. Then, we observe that the results of the model taking into account the bone and cartilage present a nearly similar trend to those of Koike et al. (Koike et al., 2002). Although we have a shift in the peak of the maximum displacement of the umbo. Indeed, Koike et al. obtained the maximum displacement around 1250 Hz, but with the 3D model of the human ear with the bone and cartilage, the peak of the maximum displacement is observed around 2500 Hz. One of the reasons that could explain this shift might be the fact that Koike et al. (Koike et al., 2002) modeled the ossicular chain, the ligaments, and tendons of the middle ear and replaced the cochlea with a mechanical impedance, whereas in our model, the ossicular chain and the cochlea were represented by the impedance of a mass-spring-damper system.

5. Conclusion

This study aimed to develop a 3D human ear model to investigate how bony and cartilaginous tissues influence umbo displacement. The model includes the auditory canal, bone, skin, cartilage, and tympanic membrane (pars tensa and pars flaccida). The middle ear’s influence was accounted for by replacing the ossicular chain and cochlea with an equivalent mass-spring-damper impedance.

Our findings indicate that bone and cartilage influence the response between 2500 and 6300 Hz. A comparison with Koike et al. (Koike et al., 2002) revealed discrepancies at various frequencies, which we attribute to differences in modeling methodology. Specifically, our model simplifies the ossicular chain and cochlea into a mass-spring-damper impedance, whereas Koike et al. explicitly modeled the ossicular chain, tendons, and ligaments while representing the cochlea with an impedance. To enhance our model, future work will incorporate detailed modeling of the ossicular chain, ligaments, tendons, and cochlea

References 

240. P. Sarvazyan et al., “Biophysical Bases of Elasticity Imaging,” 1995, pp. 223–240. doi: 10.1007/978-1-4615-1943-0_23.

Bopanna B. Ballachanda, The human ear canal, Second edition. Plural Publishing, 2013.

10. M. Jenks, V. Patel, B. Bennett, B. Dunham, and C. M. Devine, “Development of a 3‐Dimensional Middle Ear Model to Teach Anatomy and Endoscopic Ear Surgical Skills,” OTO Open, vol. 5, no. 4, Oct. 2021, doi: 10.1177/2473974X211046598.

C.-F. Lee, P.-R. Chen, W.-J. Lee, J.-H. Chen, and T.-C. Liu, “Three-Dimensional Reconstruction and Modeling of Middle Ear Biomechanics by High-Resolution Computed Tomography and Finite Element Analysis,” Laryngoscope, vol. 116, no. 5, pp. 711–716, May 2006, doi: 10.1097/01.mlg.0000204758.15877.34.

Cox RW and Peacock MA, “The growth of elastic cartilage,” J Anat, vol. 128(Pt 1), pp. 207–213, Jan. 1979.

10. A. G. Shaw and M. R. Stinson, “Network concepts and energy flow in the human middle‐ear,” J Acoust Soc Am, vol. 69, no. S1, pp. S43–S43, May 1981, doi: 10.1121/1.386273.
11. T. Perry and W. B. Shelley, “The Histology of the Human Ear Canal with Special Reference to the Ceruminous Gland1,” Journal of Investigative Dermatology, vol. 25, no. 6, pp. 439–451, Dec. 1955, doi: 10.1038/jid.1955.149.

Ernest Glen Wever and Merle Lawrence, Physiological Acoustics. 1954.

10. Liu, L. Xue, J. Yang, G. Cheng, L. Zhou, and X. Huang, “Effect of ossicular chain deformity on reverse stimulation considering the overflow characteristics of third windows,” Comput Methods Biomech Biomed Engin, vol. 25, no. 3, pp. 257–272, Feb. 2022, doi: 10.1080/10255842.2021.1948023.
11. Peterson and P. C. Dechow, “Material properties of the human cranial vault and zygoma,” Anat Rec, vol. 274A, no. 1, pp. 785–797, Sep. 2003, doi: 10.1002/ar.a.10096.

John Cameron, Physical properties of tissue. A comprehensive reference book, edited by Francis A. Duck. 1991.

10. K. Brummund, F. Sgard, Y. Petit, and F. Laville, “Three-dimensional finite element modeling of the human external ear: Simulation study of the bone conduction occlusion effect,” J Acoust Soc Am, vol. 135, no. 3, pp. 1433–1444, Mar. 2014, doi: 10.1121/1.4864484.
11. R. Stinson and B. W. Lawton, “Specification of the geometry of the human ear canal for the prediction of sound‐pressure level distribution,” J Acoust Soc Am, vol. 85, no. 6, pp. 2492–2503, Jun. 1989, doi: 10.1121/1.397744.
12. P. Daphalapurkar, C. Dai, R. Z. Gan, and H. Lu, “Characterization of the linearly viscoelastic behavior of human tympanic membrane by nanoindentation,” J Mech Behav Biomed Mater, vol. 2, no. 1, pp. 82–92, Jan. 2009, doi: 10.1016/j.jmbbm.2008.05.008.
13. Delille, D. Lesueur, P. Potier, P. Drazetic, and E. Markiewicz, “Experimental study of the bone behaviour of the human skull bone for the development of a physical head model,” International Journal of Crashworthiness, vol. 12, no. 2, pp. 101–108, Aug. 2007, doi: 10.1080/13588260701433081.
14. Z. Gan, B. Feng, and Q. Sun, “Three-Dimensional Finite Element Modeling of Human Ear for Sound Transmission,” Ann Biomed Eng, vol. 32, no. 6, pp. 847–859, Jun. 2004, doi: 10.1023/B:ABME.0000030260.22737.53.

T. Koike, H. Wada, and T. Kobayashi, “Modeling of the human middle ear using the finite-element method,” J Acoust Soc Am, vol. 111, no. 3, pp. 1306–1317, Mar. 2002, doi: 10.1121/1.1451073.

10. Grellmann et al., “Determination of strength and deformation behavior of human cartilage for the definition of significant parameters,” J Biomed Mater Res A, vol. 78A, no. 1, pp. 168–174, Jul. 2006, doi: 10.1002/jbm.a.30625.
11. Zhang and R. Z. Gan, “Finite element modeling of energy absorbance in normal and disordered human ears,” Hear Res, vol. 301, pp. 146–155, Jul. 2013, doi: 10.1016/j.heares.2012.12.005.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MJHI and/or the editor(s). MJHI and/or the editor(s) disclaim responsibility for any injury to

people or property resulting from any ideas, methods, instructions or products referred to in the content.